 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> VI, 1995 >> Турнир матбоёв >> Высшая лига >> 1-й тур | Убрать решения |
|
|
| VI Всероссийский фестиваль юных математиков. Анапа. 1995. Турнир матбоёв. Высшая лига. 1-й тур |
|
|
Решение: Нет, не может. Задача 2: Труппа из 16 человек играет пьесу, в которой 16 ролей. Один актер в каждом спектакле играет ровно одну роль, и роли у каждого актера не повторяются в одном сезоне. Труппа заканчивает сезон, когда нельзя подобрать роли актерам, удовлетворяющие этому требованию. Может ли труппа закончить сезон быстрее, чем за 16 спектаклей?
Задача 3: Можно ли разрезать куб на 6 равных треугольных пирамид?
Задача 4: Докажите, что если произведение положительных чисел a, b и c равно единице, то
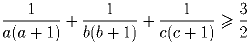
Задача 5: Функция удовлетворяет функциональному уравнению 4f(f(x)) = 2f(x) + x. Докажите, что f(x) = 0 тогда и только тогда, когда x = 0.
Решение: Пусть f(a) = 0. Тогда подставим вместо x значения a, 0, a/4, a/8. Легко получаем, что a = 0. Пусть f(0) = a. Подставляем вместо x значения 0, a, a/2. Получаем a = 0.
Задача 6: Все точки полосы ширины 0,001 раскрашены в два цвета. Докажите, что найдутся две точки одного цвета на расстоянии 1. Задача 7: В клетки квадратной таблицы 2n × 2n записаны целые числа. Известно, что таблица 2 × 2n, составленная из любых двух строк исходной таблицы, содержит n столбцов с четной суммой и n столбцов – с нечетной. Докажите, что таблица 2n × 2, составленная из любых двух столбцов, содержит n строк с четной суммой и n – с нечетной.
Задача 8: Для данного натурального числа N построим две последовательности (an) и (bn): a1 = b1 = N, an + 1 = an + S(an), bn + 1 = bn + Π (bn), где S(m) – сумма цифр, Π (m) – произведение цифр натурального m. Докажите, что при каждом N найдется такой номер k, что a1 > b1. Решение: Достаточно доказать, что, начиная с некоторого момента, последовательность (bn) перестанет возрастать, в то время как (an) постоянно возрастает. Задача 9: Два игрока играют в «уголки-квадратики". У одного игрока мешок уголков
 , у другого – мешок квадратиков
, у другого – мешок квадратиков  (сторона любого квадратика 1). Один из игроков выкладывает несколько
(по крайней мере одну) фигурок из своего мешка, а затем другой
добавляет по своему выбору несколько своих фигурок. Начинающий
выигрывает, если из полученного набора уголков и квадратиков можно
составить прямоугольник, и проигрывает в противном случае. Верно ли,
что у одного из игроков есть выигрышная стратегия независимо от того,
кто начинает игру?
Решение:
Всегда выигрывает участник, играющий «квадратиками". Если
он ходит первым, то ему достаточно выложить три квадратика – тогда
при любом ответе второго игрока он сможет выложить прямоугольник либо
2 × k, либо 3 × k. Если же он играет вторым, то он должен
дополнить своими квадратиками утроенное количество фигурок первого
игрока до ближайшего простого числа – тогда общее количество
элементарных квадратиков будет простым числом, и сложить
прямоугольник не удастся.
Задача 10:
Внутри треугольника ABC взяты точки P, Q и R. Известно,
что пары отрезков AQ и BP, BR и CQ, CP и AR пересекаются
соответственно в точках H, F и G так, что AH = AG, BH = BF, CF = CG и
∠ AHP = ∠ BFQ = ∠ CGR. Докажите, что прямые PF, QG и
RH пересекаются в одной точке.
(сторона любого квадратика 1). Один из игроков выкладывает несколько
(по крайней мере одну) фигурок из своего мешка, а затем другой
добавляет по своему выбору несколько своих фигурок. Начинающий
выигрывает, если из полученного набора уголков и квадратиков можно
составить прямоугольник, и проигрывает в противном случае. Верно ли,
что у одного из игроков есть выигрышная стратегия независимо от того,
кто начинает игру?
Решение:
Всегда выигрывает участник, играющий «квадратиками". Если
он ходит первым, то ему достаточно выложить три квадратика – тогда
при любом ответе второго игрока он сможет выложить прямоугольник либо
2 × k, либо 3 × k. Если же он играет вторым, то он должен
дополнить своими квадратиками утроенное количество фигурок первого
игрока до ближайшего простого числа – тогда общее количество
элементарных квадратиков будет простым числом, и сложить
прямоугольник не удастся.
Задача 10:
Внутри треугольника ABC взяты точки P, Q и R. Известно,
что пары отрезков AQ и BP, BR и CQ, CP и AR пересекаются
соответственно в точках H, F и G так, что AH = AG, BH = BF, CF = CG и
∠ AHP = ∠ BFQ = ∠ CGR. Докажите, что прямые PF, QG и
RH пересекаются в одной точке.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> VI, 1995 >> Турнир матбоёв >> Высшая лига >> 1-й тур | Убрать решения |