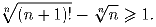Задача 1: На планете, имеющей форму шара с длиной экватора d,
расположено n > 3 аэродромов. Известно, что по разные стороны от
любой «экваториальной» плоскости есть хотя бы один аэродром.
Назовем два аэродрома далекими, если расстояние между ними по
поверхности не меньше
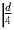
. Докажите, что если любые два далеких
аэродрома связаны прямым авиарейсом, то с каждого аэродрома можно
долететь до любого другого (возможно с пересадками).
Задача 2: Докажите, что для любого натурального выполнено неравенство
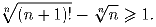
Задача 3: Каждый из 26 единичных кубиков куба 3 × 3 × 3
покрашен
первоначально в черный или белый цвет (центральный кубик исключен).
За один ход разрешается, выбрав любой из кубиков, перекрасить его и
все соседние с ним по граням кубики в противоположные цвета.
Докажите, что из любой первоначальной раскраски кубика можно
получить любую наперед заданную раскраску за конечное число ходов.
Задача 4: Вершины A и B треугольника ABC лежат на окружности, а вершина
C – внутри этой окружности. В криволинейный треугольник ABC вписана
окружность, касающаяся дуги AB в точке M. Пусть S – центр вписанной
в (прямолинейный) треугольник ABC окружности, N – середина дуги AB,
не содержащей точки M. Докажите, что точки M, S и N лежат на одной
прямой.
Задача 5: Какое наибольшее число ребер может иметь граф с n вершинами,
если никакие два цикла в этом графе не имеют общих вершин?
Задача 6: Имеется 64 внешне одинаковые монеты, некоторые из которых
фальшивые (но не все). Фальшивые монеты весят одинаково и отличаются
по весу от настоящих. Как за шесть взвешиваний на чашечных весах без
гирь найти две различные по весу монеты?
Задача 7: Найдите все функции f: N → Z ,
удовлетворяющие для всех x,y ∈ N равенству
f(xy) = f(x) + f(y) – f(d(x,y)),
где d(x,y) – наибольший общий делитель чисел x и y.
Задача 8: Точки A, B, C взяты на сторонах B
1C
1, C
1A
1,
A
1B
1 треугольника
A
1B
1C
1, причем ABC = A
1B
1C
1, BCA = B
1C
1A
1, CAB = C
1A
1B
1.
Докажите, что
ортоцентры треугольников ABC и A
1B
1C
1 равноудалены от центра
описанной окружности треугольника ABC.
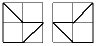
9. Докажите, что из набора, содержащего фигурки указанного вида,
нельзя сложить ни один прямоугольник со сторонами, параллельными
линиям сетки. (Фигурки состоят из единичного квадрата с двумя
приклеенными «ногами» в виде равнобедренных прямоугольных
треугольников. Стороны единичного квадрата ориентированы по линиям
сетки).
Задача 10: На плоскости даны окружностей одинакового радиуса, каждая
из которых пересекается хотя бы с одной другой; касающихся
окружностей нет. Докажите, что различных точек пересечений
окружностей не меньше n.


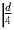 . Докажите, что если любые два далеких
аэродрома связаны прямым авиарейсом, то с каждого аэродрома можно
долететь до любого другого (возможно с пересадками).
Задача 2: Докажите, что для любого натурального выполнено неравенство
. Докажите, что если любые два далеких
аэродрома связаны прямым авиарейсом, то с каждого аэродрома можно
долететь до любого другого (возможно с пересадками).
Задача 2: Докажите, что для любого натурального выполнено неравенство