Задача 1: Докажите, что для любого натурального n ≥ 3 существуют арифметическая прогрессия a₁,a₂, … a_n и геометрическая прогрессия b₁,b₂, … b_n, состоящие из натуральных чисел, такие, что b₁ < a₁ < b₁ <  …  < b_n < a_n.

Задача 2: Найдите минимальный радиус бесконечного кругового цилиндра, который содержит правильный октаэдр со стороной a.

Задача 3: В теннисном клубе n теннисистов a₁, a₂, …, a_n. Для участия в парных состязаниях они образовали n пар K₁, K₂, …, K_n. Известно, что среди этих пар есть пара (a_i,a_j) тогда и только тогда, когда в парах K_i и K_j есть один общий теннисист. Докажите, что каждый теннисист участвует ровно в двух парах.

Задача 4: Можно ли квадрат со стороной 5 расположить на координатной плоскости так, что он покроет 21 целочисленную точку (квадрат с границей).

Задача 5: Найдите все натуральные n, для которых существует целое m такое, что m² + 9 делится на 2ⁿ – 1.

Задача 6: Найдите все натуральные n ≥ 3 такие, что наибольшее число точек с попарными расстояниями, большими 1, расположенных внутри или на границе правильного n-угольника со стороной 1, равно n – 1.

Задача 7: Рассмотрим наборы длины n, состоящие из 0 и 1. Назовем расстоянием d(M,N) между двумя такими наборами M и N число позиций, в которых наборы не совпадают. Докажите, что если для трех наборов A, B, C d(A,B) = d(B,C) = d(C,A) = R, то существует набор D, для которого d(A,D) = d(B,D) = d(C,D) = R/2.

Задача 8: Докажите, что при n ≥ 3 для любого набора чисел 0 ≤ a₁ ≤ a₂ ≤  …  ≤ a_n выполняется неравенство .

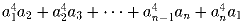
Задача 9: Даны две неравные окружности, расположенные одна вне другой. Пусть точка O – точка пересечения их общих внешних касательных. Через O проводится прямая, пересекающая окружности в точках A,B,C,D (точки перечислены в порядке удаления от O). Из точек A и D проводятся по две касательные к окружностям, на которых они не лежат. Эти касательные высекают в окружностях по криволинейному треугольнику. Докажите, что радиусы окружностей, вписанных в эти криволинейные треугольники, равны.

Задача 10: Найдите все функции f: R  →  R , удовлетворяющие уравнению f(x²) – f(y²) = (x + y)(f(x) – f(y)) для всех x,y ∈  R .
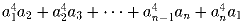