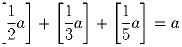Задача 1: Найдите число действительных решений уравнения
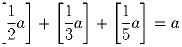
([x] – целая часть числа x).
Задача 2: Пусть I – центр окружности, вписанной в треугольник ABC,
а
I
1, I
2, I
3 – центры окружностей, вписанных в треугольники
IBC, AIC, ABI соответственно.
Докажите, что прямые AI
1, BI
2, CI
3 пересекаются
в одной точке.
Задача 3: Для множества A, состоящего из натуральных чисел, обозначим
через n
A количество троек (x,y,z) элементов A таких, что x < y
и x + y = z. Найдите максимальное значение n
A для множеств A,
содержащих семь различных элементов.
Задача 4: На отрезке, соединяющем центры двух вневписанных окружностей
треугольника, выбрана такая точка, что касательные, проведенные из
нее к указанным окружностям, равны. Докажите, что прямая, проходящая
через эту точку перпендикулярно данному отрезку, делит периметр
треугольника пополам.
Задача 5: Найдите все простые p, для которых числа p + 1 и
p² + 1 являются удвоенными квадратами натуральных чисел.
Задача 6: Найдите все пары единичных кубиков, составляющих куб 8 × 8 × 8
при выбрасывании которых оставшуюся часть можно разрезать на блоки
1 × 1 × 2.
Задача 7: Найдите все функции f: R → R , удовлетворяющие уравнению
f(f(x) + y) = f(x² – y) + 4yf(x)
для всех x,y ∈ R .
Задача 8: Два велосипедиста стартуют одновременно из двух точек
круговой велотрассы: первый из точки A, второй из точки B -–
и едут в противоположных направлениях с постоянными скоростями. Известно, что
из первых 15 встреч на трассе после старта только третья и
пятнадцатая состоялись в точке B. Найдите отношение скорости первого
велосипедиста к скорости второго, если известно, что к моменту их
пятой встречи каждый из велосипедистов проехал не менее одного
круга.
Задача 9: Два игрока играют на доске m × n в следующую игру. У них есть
белый и черный король соответственно, стоящие в противоположных
углах доски. Они передвигают своих королей (по правилам шахмат)
поочередно так, чтобы расстояние между центрами клеток, на которых
стоят короли, уменьшалось (королям разрешается занимать соседние
клетки). Проигрывает тот, кто не может сделать ход. Кто выигрывает
при правильной игре?
Задача 10: Можно ли расположить на плоскости девять отрезков так, чтобы каждый
пересекался ровно с четырьмя другими?