 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> I, 1990 >> Турнир матбоёв >> 1-й тур | Убрать решения |
|
|
| I Всероссийский фестиваль юных математиков. Краснодар. 1990. Турнир матбоёв. 1-й тур |
|
|
Задача 2: Существует ли такое n, что любое рациональное число между 0 и 1 представимо в виде
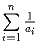 , где
ai – натуральные числа?
, где
ai – натуральные числа?Решение: Сформулируем вспомогательную Лемму. Пусть число слагаемых n фиксировано. Тогда для любого числа α n можно указать такое число β n < α n, что если
 , то
, то
 . Эту Лемму несложно доказать индукцией по
n. (Базу проверим при n = 1:
. Эту Лемму несложно доказать индукцией по
n. (Базу проверим при n = 1:  .
Легко делается и шаг индукции.) Теперь применим нашу Лемму при
α n = 1. Получим, что при каждом n существует некоторый
интервал ( α n, β n), ни одно из чисел которого не
представимо в требуемом виде. Но понятно, что в этом интервале
найдется хотя бы одно (и даже бесконечно много!) рациональное число.
Задача 3:
Сколькими способами ладья может с поля a1 попасть на поле h6,
двигаясь только вправо и вверх?
.
Легко делается и шаг индукции.) Теперь применим нашу Лемму при
α n = 1. Получим, что при каждом n существует некоторый
интервал ( α n, β n), ни одно из чисел которого не
представимо в требуемом виде. Но понятно, что в этом интервале
найдется хотя бы одно (и даже бесконечно много!) рациональное число.
Задача 3:
Сколькими способами ладья может с поля a1 попасть на поле h6,
двигаясь только вправо и вверх?Решение: Заметим, что ладье нужно сделать 7 единичных ходов вправо и 5 единичных ходов вверх; причем эти ходы можно чередовать в любом порядке, и при этом будут перебраны все возможные варианты движения ладьи. Значит, ответ
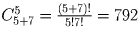 .
Задача 4:
Докажите, что
.
Задача 4:
Докажите, что
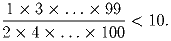
Решение: По индукции легко доказать, что

Задача 7: Докажите, что n! не делится на 2n ни при каком натуральном n.
Решение: Пусть n = 2k + t, где t – нечетное. Тогда количество двоек в разложении n! на простые сомножители равно

Решение: Например, индукцией по числу вершин. Задача 9: На сторонах треугольника ABC во внешнюю сторону построены квадраты ABMP и BCDK. Докажите, что продолжение медианы BE треугольника ABC является высотой треугольника BMK.
Решение: Повернем треугольник ABC на 90 относительно точки B так, чтобы точка A перешла в точку M. Пусть при этом C перейдет в C′. Но тогда BE перейдет в среднюю линию треугольника MC′K. Задача 10:
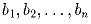 – некоторая перестановка чисел
– некоторая перестановка чисел
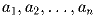 . Докажите, что
. Докажите, что
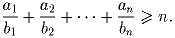
Решение: Например, по неравенству Коши.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> I, 1990 >> Турнир матбоёв >> 1-й тур | Убрать решения |