 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> I, 1990 >> Турнир матбоёв >> Дополнительный матбой ``Москва -- Бургас'' | Показать решения |
|
|
| I Всероссийский фестиваль юных математиков. Краснодар. 1990. Турнир матбоёв. Дополнительный матбой ``Москва -- Бургас'' |
|
|
Задача 2: Можно ли на окружности единичного радиуса отметить 1990 точек так, чтобы длина любой соединяющей их хорды была рациональной?
Задача 3: Квадрат разбит на два конгруэнтных многоугольника. Докажите, что центр квадрата лежит на их границе.
Задача 4: На бесконечной ленте напечатана бесконечная последовательность цифр от 1 до 9. Докажите, что либо какая-то комбинация цифр повторится 10 раз подряд, либо из нее можно вырезать 10 стозначных чисел идущих в порядке убывания.
Задача 5: Докажите, что для любой точки O внутри квадрата ABCD выполняются неравенства: 135 < ∠ OAB + ∠ OBC + ∠ OCD + ∠ ODA < 225.
Задача 6: На окружности записаны 128 целых чисел. За один ход между каждой парой соседних чисел записывается их сумма, а сами эти числа стираются. Докажите, что через несколько ходов все числа будут делиться на 128.
Задача 7: Прямая раскрашена в 2 цвета. Докажите, что найдутся три точки A1, A2, A3 одного цвета, такие, что A1A2 = A2A3.
Задача 8: Решите уравнение:
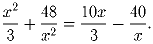
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> I, 1990 >> Турнир матбоёв >> Дополнительный матбой ``Москва -- Бургас'' | Показать решения |