Задача 1: Докажите, что если последняя цифра числа n не нуль, то существует целое k, такое, что в десятичной записи числа kn нет ни одного нуля.

Задача 2: Написано 20 чисел от 1 до 20. Двое играющих ставят перед этими числами знаки « + " или « – " (знак можно ставить перед любым свободным числом). Первый стремится к тому, чтобы полученная в конце сумма была как можно меньше по модулю. Какую максимальную сумму может себе обеспечить второй?

Задача 3: A₁, A₂, …, A_n и B₁, B₂, …, B_n – два разбиения единичного квадрата на непересекающиеся множества. S_ij – пересечение множеств A_i и B_j. |G| – площадь множества G. Докажите неравенство:

Задача 4: Треугольник ABC разрезан на треугольнички триангуляции так, что соприкасающиеся треугольнички имеют либо общую вершину, либо общую сторону. Отображение F переводит треугольник ABC в треугольник A₁B₁C₁ – вершины в вершины, а стороны в стороны – и линейно на треугольничках триангуляции (т.е. отрезок, лежащий внутри или на стороне треугольничка, переводит в отрезок). Докажите, что каждая точка в треугольнике A₁B₁C₁ имеет нечетное число прообразов, либо имеет прообраз, лежащий на стороне треугольничка.

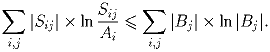
Задача 5: В пространстве расположено несколько плоскостей общего положения (никакие три не параллельны одной прямой, и все не пересекаются в одной точке). Они делят пространство на несколько частей и в каждой части записан знак: плюс или минус. Разрешается изменить все знаки во всех частях внутри любого тетраэдра. Докажите, что за несколько операций можно сделать так, чтобы во всех ограниченных частях стояли плюсы.

Задача 6: На плоском столе лежат круглые салфетки. Докажите, что если любые две перекрываются, то все салфетки можно прибить к столу с помощью 100 гвоздей.

Задача 7: Решите в целых числах неравенство: |2ⁿ – 3^m| ≤ 6

Задача 8: На сторонах AB и BC произвольного треугольника ABC строятся два произвольных параллелограмма. Их стороны, противоположные сторонам треугольника, продолжаются до пересечения в точке S. На стороне AC строится параллелограмм, две стороны которого равны и параллельны BS. Докажите, что площадь третьего параллелограмма равна сумме площадей первых двух.