 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> I, 1990 >> Турнир матбоёв >> 1-й тур | Показать решения |
|
|
| I Всероссийский фестиваль юных математиков. Краснодар. 1990. Турнир матбоёв. 1-й тур |
|
|
Задача 2: Существует ли такое n, что любое рациональное число между 0 и 1 представимо в виде
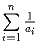 , где
ai – натуральные числа?
, где
ai – натуральные числа?Задача 3: Сколькими способами ладья может с поля a1 попасть на поле h6, двигаясь только вправо и вверх?
Задача 4: Докажите, что
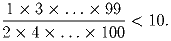
Задача 5: В прямоугольной таблице стоят натуральные числа. Разрешается одновременно вычесть 1 из всех чисел одной строки или умножить на 2 все числа одного столбца. Докажите, что с помощью этих операций можно получить таблицу из одних нулей. Задача 6: На плоскости заданы прямая L и две точки A и B. Как следует выбрать на этой прямой точку P, чтобы наибольшее из расстояний AP и BP было минимальным?
Задача 7: Докажите, что n! не делится на 2n ни при каком натуральном n.
Задача 8: Докажите, что сумма плоских углов выпуклого замкнутого многогранника равна 360 × (n – 2), где n – число вершин.
Задача 9: На сторонах треугольника ABC во внешнюю сторону построены квадраты ABMP и BCDK. Докажите, что продолжение медианы BE треугольника ABC является высотой треугольника BMK.
Задача 10:
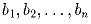 – некоторая перестановка чисел
– некоторая перестановка чисел
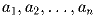 . Докажите, что
. Докажите, что
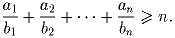
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> I, 1990 >> Турнир матбоёв >> 1-й тур | Показать решения |