 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> II, 1991 >> Турнир матбоёв >> Финал | Показать решения |
|
|
| II Всероссийский фестиваль юных математиков. Краснодар. 1991. Турнир матбоёв. Финал |
|
|
Задача 2:
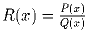 – отношение двух многочленов
степени m без общих корней. Высотой h( α ) рационального
числа α назовем сумму модулей числителя и знаменателя его
представления в виде несократимой дроби плюс 1. Докажите, что при
некотором c > 0 имеет место неравенство:
h(R( α )) > hnc( α ).
– отношение двух многочленов
степени m без общих корней. Высотой h( α ) рационального
числа α назовем сумму модулей числителя и знаменателя его
представления в виде несократимой дроби плюс 1. Докажите, что при
некотором c > 0 имеет место неравенство:
h(R( α )) > hnc( α ).Задача 3: Последовательность a1, a2, … . такова, что |a1| = 1 и |ai + 1| = |ai + 1| для k ≥ 1. Найдите наименьшее возможное значение модуля суммы
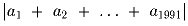 .
.Задача 4: Внутри выпуклого многогранника объемом 1 отмечено 3(2n – 1) точки. Докажите, что из него можно вырезать выпуклый многогранник объема
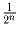 , не содержащий внутри себя ни одной отмеченной
точки.
, не содержащий внутри себя ни одной отмеченной
точки.Задача 5: Докажите, что любую функцию, определенную на всей числовой прямой, можно представить в виде суммы двух функций, график каждой из которых имеет центр симметрии.
Задача 6: В числовом треугольнике верхнее число равно 1, а крайние числа в каждой строке тоже, равны 1. Каждое из остальных чисел не меньше суммы двух чисел, стоящих над ним. Пусть натуральное число a > 1 встречается в треугольнике k раз. Докажите, что 2k < a².
Задача 7: Докажите, что если 8k + 1 – простое, то при некотором q число q² – 2 делится на 8k + 1.
Задача 8: Найдите все такие геометрические прогрессии, n и k, что сумма n последовательных первых членов этой геометрической прогрессии делит сумму их k-х степеней.
Задача 9: Можно ли разбить квадрат на непересекающиеся отрезки, из которых можно сложить квадрат других размеров?
Задача 10: Какому условию должны удовлетворять длины сторон треугольника, чтобы треугольник, составленный из его медиан был подобен данному?
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> II, 1991 >> Турнир матбоёв >> Финал | Показать решения |