 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> II, 1991 >> Турнир матбоёв >> 4-й тур | Убрать решения |
|
|
| II Всероссийский фестиваль юных математиков. Краснодар. 1991. Турнир матбоёв. 4-й тур |
|
|
Задача 2: В четырехугольнике все стороны и диагонали не длиннее одного сантиметра. Каков наибольший возможный периметр этого четырехугольника?
Задача 3: Может ли произведение трех последовательных натуральных чисел равняться некоторой степени натурального числа (квадрату, кубу и т.д.)?
Решение: Нет, не может. Воспользуйтесь взаимной простотой k + 1 и k(k + 2). Задача 4: В стране Плюралии 1990 политических партий. В каждой состоит более половины населения. Докажите, что начальнику тайной полиции хватит 10 осведомителей, чтобы получать информацию о деятельности всех партий.
Решение: Построим прямоугольный параллелепипед, три ребра которого идут по осям цилиндров. Поместим начало системы координат в центр параллелепипеда, а оси направим параллельно его сторонам. Для точки с координатами (x,y,z) запишем условие принадлежности всем трем цилиндрам. Сложим три получившихся неравенства. Легко получить, что
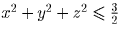 .
Задача 5:
Докажите, что пересечение трех прямых круговых цилиндров радиуса
1, оси которых попарно взаимно перпендикулярны (но не обязательно
пересекаются) содержится в некотором шаре радиуса
.
Задача 5:
Докажите, что пересечение трех прямых круговых цилиндров радиуса
1, оси которых попарно взаимно перпендикулярны (но не обязательно
пересекаются) содержится в некотором шаре радиуса 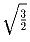 .
.Задача 6: В каждой клетке шахматной доски написано целое число от 1 до 64, причем в разных клетках – разные числа. За один вопрос можно указать любое множество полей и узнать совокупность стоящих в них чисел. За какое наименьшее число вопросов можно узнать число в каждой клетке?
Решение: Наименьшее необходимое число вопросов равно 6. Задача 7: На координатной плоскости даны три системы прямых: x = n, y = m, x + y = k, где m, n, k – целые. Плоскость ими разбивается на части, некоторые из которых – треугольники. Пусть T(R) – это число треугольных частей, а M(R) – общее число частей, лежащее в круге x² + y² = R. Найдите
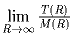 .
.Задача 8: Назовем выпуклый многоугольник константным, если сумма расстояний от точки внутри него до прямых, содержащих стороны, постоянна. Докажите, что многоугольник A1A2 … An константен тогда и только тогда, когда

Задача 9: Докажите, что 1¹ºº + 2¹ºº + ... + 999999¹ºº делится на 100000.
Решение: Разобьем слагаемые на пары (a¹ºº,(106 – a)¹ºº). Эти пары разобьем на 5 групп, в каждой из которых a изменяется от k × 105 + 1 до (k + 1) × 105, k = 0,1,2,3,4. Легко видеть, что сумма пар в каждой группе равноостаточна с суммой 1¹ºº + 2¹ºº + + … + 99999¹ºº. Осталось доказать, что 1¹ºº + 2¹ºº + … + 99999¹ºº делится на 10000. Повторяя рассуждения, спускаемся к очевидному факту: 1¹ºº + … + 99¹ºº делится на 10. Задача 10: В последовательности an (n = 1,2, … ) a1 – произвольное натуральное число, а каждое следующее число равно предыдущему, сложенному с суммой его цифр. Докажите, что при бесконечно многих значениях n сумма цифр числа an не превосходит
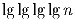 .
.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> II, 1991 >> Турнир матбоёв >> 4-й тур | Убрать решения |