 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> III, 1992 >> Турнир матбоёв >> 1-й тур | Показать решения |
|
|
| III Всероссийский фестиваль юных математиков. Краснодар. 1992. Турнир матбоёв. 1-й тур |
|
|
Задача 2: Обозначим через a(n) число способов, которыми данное натуральное число n можно представить в виде суммы нескольких (быть может, одного) натуральных слагаемых, больших единицы, с учетом их порядка. Докажите для каждого n тождество: a(2) + a(4) + ... + a(2n) = a(2n + 1).
Задача 3: Найдите все многочлены P(x) такие, что для каждого x выполняется равенство: xP(x – 1) = (x – 10)P(x).
Задача 4: Пусть an – число нулей, которыми оканчивается число n! = 1 × 2 × … × n в десятичной записи. Докажите, что существует
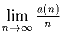 и
вычислите его.
Задача 5:
Докажите, что алгебраическое уравнение xn + a1xn – 1 + an – 1x + an = 0, среди коэффициентов которого встречаются только
числа ± 1 и 0, не имеет действительных корней, модуль которых
превышает 2.
и
вычислите его.
Задача 5:
Докажите, что алгебраическое уравнение xn + a1xn – 1 + an – 1x + an = 0, среди коэффициентов которого встречаются только
числа ± 1 и 0, не имеет действительных корней, модуль которых
превышает 2.Задача 6: Центры трех попарно касающихся внешним образом окружностей лежат в вершинах прямоугольного треугольника. Найдите радиус четвертой окружности, касающейся трех данных и содержащей их внутри себя, если периметр треугольника равен p.
Задача 7: На плоскость положили четыре прямых круговых конуса с общей вершиной и одинаковой образующей (но, вообще говоря, с различными радиусами основания) так, что каждый касается двух других. Докажите, что точки касания их оснований лежат на одной окружности.
Задача 8: Десять волейбольных команд сыграли между собой турнир в один круг. За выигрыш давалось одно очко, за проигрыш – 0. Докажите, что если команда, занявшая i-е место, набрала xi очков, то x1 + 2x2 + ... + 10x10 ≥ 165.
Задача 9: В США, начиная с 1950 года, издается журнал «Journal of Unclear Physics", который выпускается нерегулярно, но не реже, чем 5 номеров за три года. Докажите, что если журнал будет издаваться достаточно долго, то в некотором году его номер совпадет с номером года.
Задача 10: Докажите, что при каждом целом k ≥ 0 число 26k + 1 + 36k + 1 + 56k + 1 делится на 7.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> III, 1992 >> Турнир матбоёв >> 1-й тур | Показать решения |