 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> III, 1992 >> Турнир матбоёв >> 2-й тур | Показать решения |
|
|
| III Всероссийский фестиваль юных математиков. Краснодар. 1992. Турнир матбоёв. 2-й тур |
|
|
Задача 2: Дан полукруг и прямая a, перпендикулярная его диаметру AB и удаленная на расстояние AB от точки B; к полукругу проведена касательная в точке K, пересекающая прямую a в точке M. Через точку B проведена прямая, параллельная AK, до пересечения с KM в точке N. Докажите, что произведение длин отрезков KN и MN не зависит от выбора точки K.
Задача 3: Делится ли число
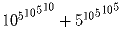 на 11?
на 11?Задача 4: За круглым столом сидят n человек, пронумерованных по порядку от 1 до n, на стульях, также пронумерованных от 1 до n, но в произвольном порядке. При каких n их всегда можно пересадить по кругу (т.е. «повернуть" относительно стульев) так, чтобы никакой номер стула, на котором сидит человек, не совпал с номером этого человека?
Задача 5: Пусть S(n) – сумма цифр числа n в десятичной записи, а σ (n) = S(1) + S(2) + ... + S(n). Докажите, что sigma(n) < 9(n + ㏑ (n!)).
Задача 6: Существует ли бесконечная последовательность из нулей и единиц, в которой никакой конечный блок не повторяется три раза подряд?
Задача 7: Докажите, что для любых десяти точек A1, … ,A10 единичной сферы с центром O среди треугольников AiAjO (1 ≤ i < j ≤ 10) найдется хотя бы один треугольник с площадью не более 0,48.
Задача 8: Две окружности пересекаются в точках A и B. AC – хорда первой окружности, касающаяся второй окружности; AD – хорда второй, касающаяся первой. Прямая CD пересекает первую окружность в точке M, отличной от точек A, B, C, D. Докажите, что прямая BM делит отрезок AD пополам.
Задача 9: Многочлен x1992 + x1991 + x1990 + x³ + x² + x + 1 разделили с остатком на многочлен x³ – 6x² + 11x – 6. Найдите этот остаток.
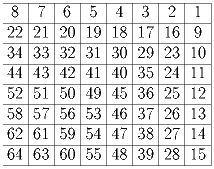
Задача 10: В таблице (n + 2) × (n + 2) по границе расставлены нули, а во внутреннем квадрате n × n – числа n^2. Для каждых двух соседних (имеющих общую сторону) клеток вычислим модуль разности стоящих в них чисел, а затем просуммируем полученные числа по всем парам соседних клеток. При каком расположении чисел n^2 эта сумма минимальна?
Задача 92: 2.10
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> III, 1992 >> Турнир матбоёв >> 2-й тур | Показать решения |