 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> III, 1992 >> Турнир матбоёв >> 4-й тур | Показать решения |
|
|
| III Всероссийский фестиваль юных математиков. Краснодар. 1992. Турнир матбоёв. 4-й тур |
|
|
Задача 2: Решите систему для положительных x,y,z:
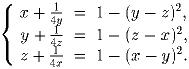
Задача 3: От прямоугольника со сторонами 1 и
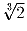 отрезают квадрат.
От оставшегося прямоугольника снова отрезают квадрат, и так далее до
бесконечности. Докажите, что отношения сторон у всех полученных
прямоугольников различны.
отрезают квадрат.
От оставшегося прямоугольника снова отрезают квадрат, и так далее до
бесконечности. Докажите, что отношения сторон у всех полученных
прямоугольников различны.Задача 4: На поверхности правильного тетраэдра найдите ГМТ концов отрезков, которые делятся пополам серединой данной высоты этого тетраэдра.
Задача 5: Для хромого шахматного коня направления, ведущие вверх, недоступны. Двое по очереди ходят им по верхней половине бесконечной шахматной доски. При каких начальных положениях коня выигрывает второй, если проигрывает тот, кому некуда ходить?
Задача 6: Дана система из 10 линейных уравнений с шестью неизвестными. Известно, что любая ее подсистема из 7 уравнений совместна. Докажите, что вся система совместна.
Задача 7: Решите уравнение 2k + 1 = pn, где n, k – натуральные, а p – простое.
Задача 8: В поселке Дивноморском 9 высотных зданий. Барон Мюнхгаузен утверждает, что всегда сможет найти место, из которого они были бы видны в заданном порядке (считая от корпуса 2 базы отдыха «Энергетик" по часовой стрелке). Не хвастает ли барон?
Задача 9: Из точки O пересечения диагоналей AC и BE правильного пятиугольника ABCDE проведены две прямые, образующие угол π /5, одна из которых пересекает сторону CD в точке M, диагональ CE – в точке L, а другая – сторону DE в точке N, а диагональ CE – в точке K. Найдите отношение площади четырехугольника KLMN к площади треугольника OKL.
Задача 10: Назовем тройку людей хорошей, если ее можно отправить в поход (так что люди не поссорятся) и плохой в противном случае. Докажите, что из бесконечного числа людей можно выбрать либо 100 человек так, чтобы любая тройка из них была хорошей, либо 100 человек так, чтобы любая тройка была плохой.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> III, 1992 >> Турнир матбоёв >> 4-й тур | Показать решения |