 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> III, 1992 >> Турнир матбоёв >> 4-й тур | Убрать решения |
|
|
| III Всероссийский фестиваль юных математиков. Краснодар. 1992. Турнир матбоёв. 4-й тур |
|
|
Решение: Сделав замену x = x1 – b/(3a), получим уравнение вида
 . А если теперь сделать замену
y1 = y – d1, то получим уравнение, график которого симметричен
относительно начала координат. Осталось заметить, что наши замены –
это параллельный перенос графика.
Задача 2:
Решите систему для положительных x,y,z:
. А если теперь сделать замену
y1 = y – d1, то получим уравнение, график которого симметричен
относительно начала координат. Осталось заметить, что наши замены –
это параллельный перенос графика.
Задача 2:
Решите систему для положительных x,y,z:
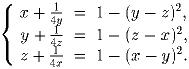
Решение: Воспользуйтесь известным неравенством:
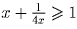 .
.Задача 3: От прямоугольника со сторонами 1 и
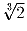 отрезают квадрат.
От оставшегося прямоугольника снова отрезают квадрат, и так далее до
бесконечности. Докажите, что отношения сторон у всех полученных
прямоугольников различны.
отрезают квадрат.
От оставшегося прямоугольника снова отрезают квадрат, и так далее до
бесконечности. Докажите, что отношения сторон у всех полученных
прямоугольников различны.Решение: Пусть λ > 1 – отношение сторон прямоугольника. Нетрудно убедиться, что при отрезании квадрата над λ могут производиться только следующие операции: вычитание единицы и взятие обратной величины. Композиция таких операций дает дробно-рациональную функцию от λ . Повторение отношений сторон означает, что λ – корень квадратного уравнения с целыми коэффициентами, что неверно. Задача 4: На поверхности правильного тетраэдра найдите ГМТ концов отрезков, которые делятся пополам серединой данной высоты этого тетраэдра.
Решение: Т.к. при симметрии отрезка относительно его середины он переходит в себя, то это ГМТ является пересечением тетраэдра с его образом при симметрии относительно середины данной высоты, и состоит из 6-звенной ломаной и концов высоты.
Задача 5: Для хромого шахматного коня направления, ведущие вверх, недоступны. Двое по очереди ходят им по верхней половине бесконечной шахматной доски. При каких начальных положениях коня выигрывает второй, если проигрывает тот, кому некуда ходить?
Решение: Воспользуйтесь методом выигрышных и проигрышных позиций. Задача 6: Дана система из 10 линейных уравнений с шестью неизвестными. Известно, что любая ее подсистема из 7 уравнений совместна. Докажите, что вся система совместна.
Задача 7: Решите уравнение 2k + 1 = pn, где n, k – натуральные, а p – простое.
Решение: Ответ: k = 3, p = 3, n = 2. Задача 8: В поселке Дивноморском 9 высотных зданий. Барон Мюнхгаузен утверждает, что всегда сможет найти место, из которого они были бы видны в заданном порядке (считая от корпуса 2 базы отдыха «Энергетик" по часовой стрелке). Не хвастает ли барон?
Решение: Порядок обзора меняется только при переходе через прямую, соединяющую два высотных здания. Надо сравнить число всех перестановок с числом частей, на которые эти прямые делят плоскость, и убедиться, что перестановок больше. Задача 9: Из точки O пересечения диагоналей AC и BE правильного пятиугольника ABCDE проведены две прямые, образующие угол π /5, одна из которых пересекает сторону CD в точке M, диагональ CE – в точке L, а другая – сторону DE в точке N, а диагональ CE – в точке K. Найдите отношение площади четырехугольника KLMN к площади треугольника OKL.
Задача 10: Назовем тройку людей хорошей, если ее можно отправить в поход (так что люди не поссорятся) и плохой в противном случае. Докажите, что из бесконечного числа людей можно выбрать либо 100 человек так, чтобы любая тройка из них была хорошей, либо 100 человек так, чтобы любая тройка была плохой.
Решение: Зафиксируем одного человека. Это позволяет называть все пары оставшихся людей хорошими ил плохими, поскольку каждую такую пару можно дополнить до тройки выделенным человеком. Выберем из оставшихся людей бесконечное подмножество так, чтобы все пары имели один тип (как это сделать – описано ниже). Зафиксируем в нем нового человека, и снова из нового множества получим еще более узкое подмножество и т.д. Получим цепочку людей и выберем из нее 100 человек первого или 100 человек второго типа, что и требовалось. Теперь покажем, как выбрать бесконечное подмножество людей, чтобы все пары имели один и тот же тип. Зафиксируем человека. Это позволит определить тип уже у людей. Возьмем бесконечное подмножество одного типа и человека в нем, и повторим ту же процедуру. Получим бесконечную цепочку людей, каждый из которых «смотрит" на предыдущих или только хорошо, или только плохо. Выберем бесконечную цепочку однотипных.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> III, 1992 >> Турнир матбоёв >> 4-й тур | Убрать решения |