 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> IV, 1993 >> Турнир матбоёв >> 2-й тур | Убрать решения |
|
|
| IV Всероссийский фестиваль юных математиков. Майкоп. 1993. Турнир матбоёв. 2-й тур |
|
|
Решение: Без ограничения общности можно считать, что x ≥ y. Но тогда при x > 3 получим x³ > 3xy. Значит, y ≤ x ≤ 3. Легким перебором убеждаемся, что подходит только пара (1,1). Задача 2: Докажите, что из любого равнобедренного треугольника площади S можно вырезать три равных треугольника площади большей, чем S/4.
Задача 3: Прямые разбивают верхнюю полуплоскость (y ≥ 0) на многоугольники, диаметр каждого из которых меньше 1. Докажите, что один из них можно выдвинуть вниз, не смещая остальные.
Задача 4: Существует ли 10000 конечных последовательностей длины 1,000,000,000
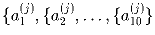 ,
j = 1,2, … ,10000 таких, что для
любого
,
j = 1,2, … ,10000 таких, что для
любого 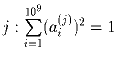 и для любых j и
k (j ≠ k):
и для любых j и
k (j ≠ k): 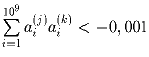 ?
?Задача 5: Каждая точка плоскости окрашена в один из трех цветов. Докажите, что по крайней мере один из этих цветов таков, что для любого d > 0 найдутся две точки этого цвета, находящиеся на расстоянии d. Решение: Допустим, что для первого цвета нет двух точек на расстоянии k. Тогда возьмем любую точку этого цвета и проведем окружность радиуса k с центром в ней. Все точки этой окружности – второго цвета, а значит, для второго цвета уже есть все расстояния от 0 до 2k. Предположим, что для второго цвета нет какого-то расстояния m > 2k. Тогда из любой точки второго цвета проведем окружность радиуса m. Все точки этой окружности имеют первый цвет. Получили противоречие с тем, что для первого цвета нет двух точек на расстоянии k. Задача 6: Найдите все функции f:R → R такие, что для любых действительных чисел a,b и c f(a + b + c) = f(a)f(b) – f(c).
Решение: Ответ: либо f ≡ 0, либо f ≡ 2. Задача 7: Сфера S вписана в правильную четырехугольную пирамиду. Сфера радиуса r вписана в трехгранный угол пирамиды, касается сферы S и находится внутри пирамиды. Сфера радиуса t вписана в четырехгранный угол пирамиды, касается сферы S и находится внутри пирамиды. Найдите радиус сферы S.
Задача 8: Диагонали выпуклого четырехугольника ABCD пересекаются в точке M, ∠ AMD = 120, AM = MD. На стороне BC взята произвольная точка E, а на сторонах AB и CD – соответственно точки K и P так, что KE\|AC и EP\|BD. Докажите, что центр окружности, описанной около треугольника KEP, лежит на стороне AD.
Задача 9: Докажите, что существует многочлен с целыми коэффициентами 1024-й степени, корнем которого является число
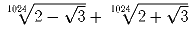 .
.Задача 10: Двое играют в такую игру. Первый пишет на доске натуральное число. Второй приписывает справа к нему некоторую цифру. Затем первый приписывает слева к получившемуся числу некоторую ненулевую цифру. Первый стремится к тому, чтобы получившееся на доске число делилось на 11, а второй хочет ему помешать. Кто выигрывает при правильной игре?
Решение: Выигрывает второй игрок. Рассмотрите два случая: второй игрок своим ходом может сделать число, делящееся на 11, либо не может, и воспользуйтесь признаком делимости на 11.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> IV, 1993 >> Турнир матбоёв >> 2-й тур | Убрать решения |