 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> IV, 1993 >> Турнир матбоёв >> 3-й тур | Показать решения |
|
|
| IV Всероссийский фестиваль юных математиков. Майкоп. 1993. Турнир матбоёв. 3-й тур |
|
|
Задача 2: В квадрате нарисованы три простые замкнутые ломаные (каждая из них может пересекать другие). Играют двое: они по очереди выбирают ломаную (каждый раз новую) и по своему желанию закрашивают часть квадрата вне или внутри нее. Первый игрок стремится к тому, чтобы в конце игры трижды закрашенная площадь была как можно меньше. Какую наименьшую площадь он может обеспечить независимо от ломаных и от игры соперника?
Задача 3: Многочлен P(x) делит xn – 1 при некотором натуральном n. Может ли один из его коэффициентов равняться 1993?
Задача 4: Две вершины параллелограмма являются серединами сторон AB и CD выпуклого четырехугольника ABCD, а две другие вершины лежат на сторонах BC и AD. Докажите, что площадь этого параллелограмма вдвое меньше площади четырехугольника ABCD.
Задача 5: В одну из клеток таблицы n × n ставится 0, в соседние (имеющие с ней общую сторону) ставятся – 1, в свободные соседние с – 1 клетки ставятся 2, затем в свободные соседние с 2 клетки ставятся – 3, затем 4, – 5, 6, и т.д. Укажите все начальные положения 0 такие, чтобы сумма всех чисел таблицы была максимальной.
Задача 6: Дан выпуклый многогранник. В каждой его вершине сходятся три грани. Каждая грань окрашена в один из 4 цветов: красный, желтый, синий или зеленый, причем грани с общим ребром – разных цветов. Докажите, что число красных граней с нечетным числом сторон имеет ту же четность, что и число синих граней с нечетным числом сторон.
Задача 7: Внутри треугольника найдите точку, для которой произведение длин перпендикуляров, опущенных из этой точки на стороны треугольника, будет наибольшим.
Задача 8: Докажите, что для любого натурального n на интервале
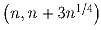 найдется число, представимое в виде суммы квадратов
двух натуральных чисел.
найдется число, представимое в виде суммы квадратов
двух натуральных чисел.Задача 9: Дано выпуклое тело в пространстве. Можно ли на его поверхности отметить 4 различные точки так, чтобы через каждую из них можно было бы провести опорную плоскость, параллельную плоскости, содержащей остальные три отмеченных точки? (Опорной называется плоскость, имеющая общие точки с границей тела, но не с его внутренностью.)
Задача 10: Дан вписанный четырехугольник ABCD. Докажите, что центры окружностей, вписанных в треугольники ABD, ABC, BCD и ACD, являются вершинами прямоугольника.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> IV, 1993 >> Турнир матбоёв >> 3-й тур | Показать решения |