 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> IV, 1993 >> Турнир матбоёв >> 4-й тур | Убрать решения |
|
|
| IV Всероссийский фестиваль юных математиков. Майкоп. 1993. Турнир матбоёв. 4-й тур |
|
|
Решение: Понятно, что придется вычеркнуть все числа, делящиеся на пять – их 19 штук. Нетрудно заметить, что произведение оставшихся чисел оканчивается на 6. Вычеркнем теперь восьмерку. Произведение оставшихся кончается либо на 2, либо на 7 (т.к. только 2 × 8 и 7 × 8 кончаются на 6). Но кончаться на 7 оно не может, так как среди сомножителей есть четные числа. Задача 2: Дана треугольная пирамида SABC; A′, B′, C′ – основания перпендикуляров, опущенных из точек A, B, C на противоположные им грани. Известно, что A′B′\|AB, B′C′\|BC и C′A′\|CA. верно ли, что пирамида правильная?
Задача 3: Прямоугольник разрезан прямыми, параллельными его сторонам, на m × n прямоугольных частей. Каждая часть покрыта карточкой, на обороте которой написана площадь этой части. Какое наименьшее число карточек надо перевернуть, чтобы определить площадь исходного прямоугольника?
Задача 4: Найдите все такие p, что уравнение
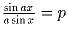 имеет решение при любом положительном a, не равном 1.
имеет решение при любом положительном a, не равном 1.Задача 5: В клетке a1 шахматной доски стоит король, который каждым ходом перемещается на 1 клетку вправо, либо вверх, либо по диагонали вправо и вверх. Двое по очереди ходят королем. Проигрывает тот, кто не может сделать очередной ход. Кто выигрывает при правильной игре?
Решение: Пометим следующие клетки доски: b2, d2, f2, h2, b4, d4, f4, h4, …, f8, h8. Первый игрок может действовать так, чтобы каждым своим ходом передвигать короля на одну из помеченных клеток; тогда второй всегда будет ходить на непомеченные клетки. Осталось заметить, что клетка h8 – помеченная. Задача 6: Каждая сторона треугольника разбита точкой, взятой на стороне, на два отрезка. Оказалось, что из полученных 6 отрезков параллельными переносами можно составить контур выпуклого шестиугольника. Докажите, что эти точки делят стороны треугольника в одинаковом отношении.
Задача 7: Каркас произвольного n-гранника спаян из металлических стержней. Найдите наименьшее число k такое, что какие бы k ребер не перекусить, многогранник распадется на отдельные части.
Задача 8: Какое наибольшее количество отрицательных чисел может быть среди чисел
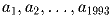 , отличных от нуля и удовлетворяющих равенству:
, отличных от нуля и удовлетворяющих равенству:
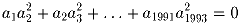
Решение: Понятно, что все числа отрицательными быть не могут – тогда сумма будет меньше нуля. Пример, когда неотрицательно только одно число, строится следующим образом. Пусть a2 = a3 = … = a1992 = – 1. Обозначим a1 = a, и пусть
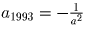 . Тогда нам достаточно убедиться в
существовании решение уравнения a5 – 19904 – a³ – 1 = 0. Но уравнение
нечетной степени всегда имеет хотя бы один действительный корень.
. Тогда нам достаточно убедиться в
существовании решение уравнения a5 – 19904 – a³ – 1 = 0. Но уравнение
нечетной степени всегда имеет хотя бы один действительный корень.Задача 9: Окружность, вписанная в четырехугольник ABCD, касается сторон AB и AD в точках E и F соответственно. Докажите, что отношение площадей треугольников ABC и ADC равно BE:DF.
Задача 10: На площади стоит несколько автомобилей. Каждый автомобиль имеет форму правильного 1993-угольника (размеры могут быть различны) и может двигаться только в направлении внешней нормали к любой из сторон. Всегда ли найдется автомобиль, который сможет выехать с площади, не задевая остальные?
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> IV, 1993 >> Турнир матбоёв >> 4-й тур | Убрать решения |