 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> VI, 1995 >> Турнир матбоёв >> Высшая лига >> 2-й тур | Показать решения |
|
|
| VI Всероссийский фестиваль юных математиков. Анапа. 1995. Турнир матбоёв. Высшая лига. 2-й тур |
|
|
 . При этом оказалось, что уголки не образовали ни
одного прямоугольника меньшей площади. Найдите все возможные пары
значений m и n.
. При этом оказалось, что уголки не образовали ни
одного прямоугольника меньшей площади. Найдите все возможные пары
значений m и n.
Задача 2: Многочлен n-й степени имеет ровно n вещественных корней (с учетом кратности). Докажите, что для всех x (P′(x))² ≥ P″(x).
Задача 3: Вдоль бесконечной дороги стоят деревья, на одном из которых сидят 1995 воробьев, на остальных деревьях воробьев вначале нет. Раз в минуту какие-либо два воробья, сидящие на одном дереве, перелетают на соседние деревья в противоположных направлениях. Воробьи начинают чирикать в тот момент, когда на каждом дереве сидит не более одного воробья. Опишите все возможные распределения воробьев по деревьям в тот момент, когда воробьи начинают чирикать.
Задача 4: Около треугольника ABC описана окружность ω . На стороне AB взята точка M. Окружность ω ′ касается изнутри окружности и касается отрезков BM и MC в точках P и Q. Докажите, что прямая PQ проходит через центр окружности, вписанной в треугольник ABC.
Задача 5: Докажите, что в десятичной записи числа
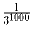 встретятся подряд цифры 1,9,9,5.
встретятся подряд цифры 1,9,9,5.Задача 6: Найдите все натуральные n такие, что каждое число, составленное из (n – 1)-й единицы и одной семерки, является простым. Задача 7: На сторонах AB, BC и CA треугольника ABC взяты соответственно точки C′, A′ и B′ так, что отрезки AA′, BB′ и CC′ пересекаются в точке K. Докажите, что A′K + B′K + C′K < max AB,BC,CA.
Задача 8: Найдите наименьшую возможную длину простой замкнутой ломаной, имеющей по крайней мере по одной общей точке с каждой гранью единичного куба. Задача 9: Найдите все последовательности (xn) такие, что при всех xn = sin xn + 1 при всех n ≥ 1.
Задача 10: Сумма неотрицательных чисел a, b, c, d и e равна единице, S = max a + b,b + c,c + d,d + e. Найдите наименьшее возможное значение S.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> VI, 1995 >> Турнир матбоёв >> Высшая лига >> 2-й тур | Показать решения |