Задача 1: Для отмывания денег N банками была разработана схема перевода
финансов, по которой каждый из этих банков был связан взаимными
переводами грязных денег с K > 2 из этих N банков.
В связи с предстоящей проверкой схему было решено изменить. Каждому банку было
предложено прекратить такие связи ровно с двумя банками. При любых
ли N и K это возможно?
Задача 2: Можно ли сложить какой-нибудь прямоугольник из набора,
содержащего четырехклеточные полоски и нечетное число
четырехклеточных уголков?
Задача 3: Квадратные трехчлены P(x) и Q(x) имеют корни. Докажите, что
по крайней мере один из трехчленов P(x) ± Q(x) также имеет корни.
Задача 4: Имеется таблица 4 × 4, в каждой клетке которой стоит 0 или 1.
Каждую минуту с ней проделывается следующая операция: для каждой
клетки считается сумма чисел в соседних с ней по сторонам клетках и
одновременно число в каждой клетке заменяется на 0, если
соответствующая сумма четна, и на 1 – если нет. Докажите, что через
6 минут какая-нибудь расстановка повторится дважды.
Задача 5: На координатной плоскости произвольно выбираются n
целочисленных точек. Пусть k – количество ненулевых отрезков с
концами в этих точках и целочисленной серединой. При каких n можно
гарантировать неравенство k > n?
Задача 6: Дано шесть трехэлементных подмножеств конечного множества X.
Докажите, что множество X можно окрасить в две краски так, что
каждое выбранное трехэлементное подмножество будет иметь точки
разных цветов.
Задача 7: Положительные числа a, b и c таковы, что ab + bc + ca ≤ 3abc.
Докажите, что a + b + c ≤ a³ + b³ + c³.
Задача 8: Фигура является объединением двух единичных квадратов с общим
центром. Какие значения может принимать отношение площади этой
фигуры к ее периметру?
Задача 9: Найдите все пары целых чисел a и b такие, что оба числа
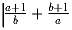
и
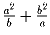
являются целыми.
Задача 10: Пусть O – точка пересечения диагоналей вписанного
четырехугольника ABCD, а K – точка, симметричная O относительно
прямой BC. Оказалось, что K лежит на описанной окружности ABCD.
Докажите, что ∠ AKO = ∠ OKD.


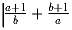 и
и 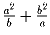 являются целыми.
Задача 10: Пусть O – точка пересечения диагоналей вписанного
четырехугольника ABCD, а K – точка, симметричная O относительно
прямой BC. Оказалось, что K лежит на описанной окружности ABCD.
Докажите, что ∠ AKO = ∠ OKD.
являются целыми.
Задача 10: Пусть O – точка пересечения диагоналей вписанного
четырехугольника ABCD, а K – точка, симметричная O относительно
прямой BC. Оказалось, что K лежит на описанной окружности ABCD.
Докажите, что ∠ AKO = ∠ OKD.