Задача 1: Для отмывания денег N банками была разработана схема перевода
финансов, по которой каждый из этих банков был связан взаимными
переводами грязных денег с K > 2 из этих N банков. В связи с
предстоящей проверкой схему было решено изменить. Каждому банку было
предложено прекратить такие связи ровно с двумя банками. При любых
ли N и K это возможно?
Задача 2: Известно, что x, y и
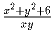
–
натуральные числа. Докажите, что x² + y² + 6 – куб натурального числа.
Задача 3: В треугольнике ABC AA
3, BB
3 и CC
3 три чевианы,
ω – вписанная окружность. Пусть A
O –
точка касания ω со стороной BC, а A
1 и A
2 –
точки пересечения AA
3 с ω , причем A
1 лежит между A и A
2.
Тройки точек
B
O, B
1, B
2 и C
O, C
1, C
2 определяются аналогично. Докажите, что точки
B
O, B
1 и точка пересечения прямых A
OA
2 и C
OC
2 лежат на одной
прямой.
Задача 4: Имеется таблица 4 × 4, в каждой клетке которой стоит 0 или 1.
Каждую минуту с ней проделывается следующая операция: для каждой
клетки считается сумма чисел в соседних с ней по сторонам клетках и
одновременно число в каждой клетке заменяется на 0, если
соответствующая сумма четна, и на 1 - если нет. Докажите, что через
6 минут какая-нибудь расстановка повторится дважды.
Задача 5: Дан многочлен P(x) с целыми коэффициентами такой, что
P( – 1) = P(1). Докажите, что существуют такие многочлены A(x) и B(x)
с
целыми коэффициентами, что при всех целых x выполняется равенство:
P(x) = A(x² – 1) + x(x² – 1)B(x² – 1).
Задача 6: На ребрах AB, BC, CD, DA параллелипипеда ABCDA
1B
1C
1D
1
произвольно выбраны точки K, L, M и N. Докажите, что центры сфер,
описанных около тетраэдров A
1AKN, B
1BKL, C
1CLM, D
1DMN
являются вершинами параллелограмма.
Задача 7: Положительные числа a, b и c таковы, что ab + bc + ca ≤ 3abc.
Докажите, что a + b + c ≤ a³ + b³ + c³.
Задача 8: На плоскости дан центрально-симметричный выпуклый
многоугольник F. Докажите, что к нему можно приложить шесть
многоугольников F
1, …, F
6, получаемых из F
параллельными
переносами так, что:
1) каждая из пар F и F1, FиF2, …, F и F6
имеет общую точку и не перекрывается;
2) фигуры F1, …, F6 попарно не перекрываются.
Задача 9: Пусть A – множество, состоящее из N различных остатков по
модулю N². Докажите, что существует множество B из N остатков по
модулю N² такое, что множество A + B = a + b|a ∈ A,b ∈ B
состоит по крайней мере из половины всех остатков по модулю N².
Задача 10: Найдите наибольшее действительное число α ,
для которого
существует бесконечная последовательность a
1, a
2, …, a
n
натуральных чисел,
удовлетворяющая следующим условиям:
(a) для каждого натурального n an > 1999ⁿ;
(b) для каждого n ≥ 2 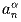 не превосходит наибольшего общего делителя
множества чисел вида ai + aj, где i + j = n.
не превосходит наибольшего общего делителя
множества чисел вида ai + aj, где i + j = n.


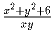 –
натуральные числа. Докажите, что x² + y² + 6 – куб натурального числа.
Задача 3: В треугольнике ABC AA3, BB3 и CC3 три чевианы,
ω – вписанная окружность. Пусть AO –
точка касания ω со стороной BC, а A1 и A2 –
точки пересечения AA3 с ω , причем A1 лежит между A и A2.
Тройки точек
BO, B1, B2 и CO, C1, C2 определяются аналогично. Докажите, что точки
BO, B1 и точка пересечения прямых AOA2 и COC2 лежат на одной
прямой.
Задача 4: Имеется таблица 4 × 4, в каждой клетке которой стоит 0 или 1.
Каждую минуту с ней проделывается следующая операция: для каждой
клетки считается сумма чисел в соседних с ней по сторонам клетках и
одновременно число в каждой клетке заменяется на 0, если
соответствующая сумма четна, и на 1 - если нет. Докажите, что через
6 минут какая-нибудь расстановка повторится дважды.
Задача 5: Дан многочлен P(x) с целыми коэффициентами такой, что
P( – 1) = P(1). Докажите, что существуют такие многочлены A(x) и B(x)
с
целыми коэффициентами, что при всех целых x выполняется равенство:
P(x) = A(x² – 1) + x(x² – 1)B(x² – 1).
Задача 6: На ребрах AB, BC, CD, DA параллелипипеда ABCDA1B1C1D1
произвольно выбраны точки K, L, M и N. Докажите, что центры сфер,
описанных около тетраэдров A1AKN, B1BKL, C1CLM, D1DMN
являются вершинами параллелограмма.
Задача 7: Положительные числа a, b и c таковы, что ab + bc + ca ≤ 3abc.
Докажите, что a + b + c ≤ a³ + b³ + c³.
Задача 8: На плоскости дан центрально-симметричный выпуклый
многоугольник F. Докажите, что к нему можно приложить шесть
многоугольников F1, …, F6, получаемых из F
параллельными
переносами так, что:
–
натуральные числа. Докажите, что x² + y² + 6 – куб натурального числа.
Задача 3: В треугольнике ABC AA3, BB3 и CC3 три чевианы,
ω – вписанная окружность. Пусть AO –
точка касания ω со стороной BC, а A1 и A2 –
точки пересечения AA3 с ω , причем A1 лежит между A и A2.
Тройки точек
BO, B1, B2 и CO, C1, C2 определяются аналогично. Докажите, что точки
BO, B1 и точка пересечения прямых AOA2 и COC2 лежат на одной
прямой.
Задача 4: Имеется таблица 4 × 4, в каждой клетке которой стоит 0 или 1.
Каждую минуту с ней проделывается следующая операция: для каждой
клетки считается сумма чисел в соседних с ней по сторонам клетках и
одновременно число в каждой клетке заменяется на 0, если
соответствующая сумма четна, и на 1 - если нет. Докажите, что через
6 минут какая-нибудь расстановка повторится дважды.
Задача 5: Дан многочлен P(x) с целыми коэффициентами такой, что
P( – 1) = P(1). Докажите, что существуют такие многочлены A(x) и B(x)
с
целыми коэффициентами, что при всех целых x выполняется равенство:
P(x) = A(x² – 1) + x(x² – 1)B(x² – 1).
Задача 6: На ребрах AB, BC, CD, DA параллелипипеда ABCDA1B1C1D1
произвольно выбраны точки K, L, M и N. Докажите, что центры сфер,
описанных около тетраэдров A1AKN, B1BKL, C1CLM, D1DMN
являются вершинами параллелограмма.
Задача 7: Положительные числа a, b и c таковы, что ab + bc + ca ≤ 3abc.
Докажите, что a + b + c ≤ a³ + b³ + c³.
Задача 8: На плоскости дан центрально-симметричный выпуклый
многоугольник F. Докажите, что к нему можно приложить шесть
многоугольников F1, …, F6, получаемых из F
параллельными
переносами так, что: 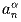 не превосходит наибольшего общего делителя
множества чисел вида ai + aj, где i + j = n.
не превосходит наибольшего общего делителя
множества чисел вида ai + aj, где i + j = n.