 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> III, 1992 >> Турнир матбоёв >> Финал | Показать решения |
|
|
| III Всероссийский фестиваль юных математиков. Краснодар. 1992. Турнир матбоёв. Финал |
|
|
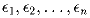 таковы, что | ε i| < 0,01 для
всех i и (1 + ε i)(1 + ε 2) … (1 + ε n) = 2.
Верно ли, что | ε 1 + ε 2 + … + ε n| < 1992?
таковы, что | ε i| < 0,01 для
всех i и (1 + ε i)(1 + ε 2) … (1 + ε n) = 2.
Верно ли, что | ε 1 + ε 2 + … + ε n| < 1992?Задача 2: Двое чеканщиков по очереди выпускают в обращение монету нового достоинства. Им запрещено чеканить копейку и любую монету, которую можно разменять монетами уже выпущенных достоинств. Проигрывает тот, кто не сможет отчеканить новую монету. Кто выигрывает при правильной игре, если первоначально никаких монет нет?
Задача 3: Пусть p – простое, p > 3, а
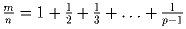 ,
где m, n – натуральные. Докажите, что m делится на p.
,
где m, n – натуральные. Докажите, что m делится на p.Задача 4: Решите систему:

Задача 5: На сфере нарисовано 1992 больших круга, никакие три из которых не пересекаются в одной точке. Докажите, что среди частей получившегося разбиения сферы найдется по крайней мере 3984 сферических треугольника. Задача 6: В клетках каждой строки таблицы n × p (n ≥ 2 – натуральное, p ≥ 3 – простое) расставлены числа от 1 до p (каждое по одному разу). Вычисляют произведение чисел в каждом столбце. При каких n из этих произведений можно всегда найти два, разность которых делится на p?
Задача 7: В пространстве даны три попарно скрещивающиеся прямые a, b и c. Каково наибольшее число прямых d таких, что d образует равные углы с a, b и c и равноудалена от них?
Задача 8: Дано конечное множество векторов на плоскости, длина каждого из которых не больше 1, а сумма равна
 . Докажите, что для любого
числа α ∈ (0;1) найдется подмножество этих векторов с суммой
. Докажите, что для любого
числа α ∈ (0;1) найдется подмножество этих векторов с суммой
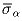 такой, что
такой, что 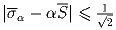 .
Задача 9:
Правильный n-угольник ориентирован по часовой стрелке. В его
вершинах расставлены цифры от 1 до 9. Для каждой пары соседних вершин
начальная служит концом, а конечная началом записи одинаковых
k-значных чисел (k < n, число k, вообще говоря, зависит от пары
вершин). Докажите, что расстановка цифр переходит в себя при
некотором повороте на угол α (0 < α < 2 π ).
.
Задача 9:
Правильный n-угольник ориентирован по часовой стрелке. В его
вершинах расставлены цифры от 1 до 9. Для каждой пары соседних вершин
начальная служит концом, а конечная началом записи одинаковых
k-значных чисел (k < n, число k, вообще говоря, зависит от пары
вершин). Докажите, что расстановка цифр переходит в себя при
некотором повороте на угол α (0 < α < 2 π ).Задача 10: Дан угол с вершиной A. На одной из его сторон взяты точки B и B1, на другой – точки C и C1 так, что отрезки BC и B1C1 пересекаются в точке K. В окружности, описанной около треугольника ABC, проведена хорда AD, параллельная B1C1, а в окружности, описанной около треугольника AB1C1, проведена хорда AD1, параллельная BC. Докажите, что точки D, D1 и K лежат на одной прямой.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> III, 1992 >> Турнир матбоёв >> Финал | Показать решения |