 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> V, 1994 >> Турнир матбоёв >> Высшая лига >> 2-й тур | Убрать решения |
|
|
| V Всероссийский фестиваль юных математиков. Михайловский. 1994. Турнир матбоёв. Высшая лига. 2-й тур |
|
|
Задача 2: Дано множество 1,2, … ,n. Для каждого его подмножества определим знакочередующуюся сумму следующим образом: расположим числа подмножества в порядке убывания и, начиная с большего числа, расставим перед ними плюсы и минусы. (Например, для n = 10 знакочередующейся суммой подмножества 1,2,4,6,9 будет 9 – 6 + 4 – 2 + 1 = 6). Найдите сумму знакочередующихся сумм всевозможных подмножеств множества 1,2, … ,n.
Решение: Понятно, что четырех таких чисел быть не может – т.к. сумма двух квадратов не может давать остаток 3 от деления на 4. Пример трех таких чисел: 72 = 6² + 6², 73 = 3² + 8², 74 = 5² + 7². Задача 3: Дан треугольник со сторонами a, b, c и полупериметром p. Строят треугольник со сторонами p – a, p – b и p – c (если он существует). Для полученного треугольника повторяют ту же процедуру, и т.д. Найдите все исходные треугольники, для которых этот процесс может продолжаться бесконечно долго.
Задача 4: Функция f:R → R такова, что при всех x f(2 + x) = f(2 – x) и f(7 + x) = f(7 – x), а f(0) = 0. Какое наименьшее число корней на отрезке [ – 1000;1000] может иметь уравнение f(x) = 0?
Решение: Докажите, что функция периодична с длиной периода 10, и что на каждом отрезке периода имеется по крайней мере 2 корня. Задача 5: На какое наименьшее число остроугольных треугольников можно разрезать правильную пятиконечную звезду?
Задача 6: Докажите, что для всех натуральных n ≥ 2 справедливо неравенство:
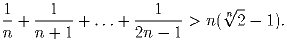
Задача 8: Двое игроков поочередно сгибают клетчатый лист бумаги размером m × n по линиям клеток. Проигрывает тот, кто не может сделать очередной ход. Кто выиграет при правильной игре: начинающий или его соперник?
Решение: Понятно, что выигрывает тот, кто первым сделает квадрат – дальше идет симметричная стратегия. Но, значит, очередная ключевая позиция – это прямоугольник n × (2n + 1): какой бы ход ни сделал первый игрок, второй всегда сможет сделать либо квадрат, либо прямоугольник такого же вида. Продолжая рассуждения, нетрудно описать множество позиций, в которых выигрывает данный игрок. Задача 9: Решите систему уравнений:
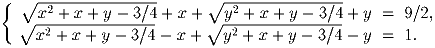
Решение: Исходная система равносильна следующей:
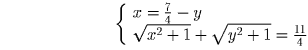
Подставив x из первого уравнения во второе, и возводя дважды в квадрат, получим квадратное уравнение относительно y. Ответ: (5/12,4/3) и (4/3,5/12).
Задача 10: Докажите, что сумма квадратов расстояний от середины стороны треугольника до его ортоцентра и до центра описанной около треугольника окружности не зависит от выбора стороны. (Ортоцентр – точка пересечения высот треугольника).Решение: Воспользуйтесь свойствами прямой Эйлера и окружности девяти точек.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> V, 1994 >> Турнир матбоёв >> Высшая лига >> 2-й тур | Убрать решения |